空が青く見えるためにはまず考えられるのは、空に青い物質が漂っているということ。それが時間とともに変化して、その結果夕方になるころには温度変化か何かで赤くなったとすれば説明がつく。しかし、今のところそのような物質は検出されていない。だいたい、もしそのような物質があれば、洗濯物が青や赤に染まってしまうではないか！そこで、太陽の影響を考えるのが妥当であろう。というのも、空の色の変化は太陽の動きに伴い、周期的に変化するからだ。太陽を原因と考えると、まずその光が疑わしくなる。すると太陽から来る光を散乱させる物質が上空になければならないことになる。なぜなら、月面から撮影した写真を思い浮かべてみると、例え撮影した場所が太陽の光の当たっているところであっても、空（？）は真っ暗である。これは月面の大気が極めて希薄なためである。地球に大気があるということから、空に色が付いているという点は説明ができた。ではなぜ昼間は青で、夕方は赤なのか？
光は電磁波である。電磁波は横波であるが、波の進行方向に物質（粒子）があった場合どうなるだろう？当然その粒子径が大きければ大きいほど（波長と比べ）、電磁波の進行方向に与える影響は大きいであろう。すなわち、散乱させやすくなる。さて、大気中に漂っている粒子で数も多く、かつ粒子径が大きいのは水蒸気の粒子である。その径は１μｍよりずっと小さい。さて、人間に見える電磁波、つまり光の波長はだいたい０．４μｍから０．８μｍである。短いほうが青、長いほうが赤である。従って、大気中の粒子の径がきわめて小さいことより、波長が短いほうが散乱されやすい。するとどうだろう。空が青いときは太陽は地面にいる人からみて、夕方よりも近い位置にある。すなわち太陽光線が大気を通り抜ける時間が短くてすむ。すると赤いほうの光は大気を通り抜けて、青い空の世界の人にはみえず、青い光は大気で散乱されて目に入ってくる。ここでもう一度注意してもらいたいのは太陽光に赤い成分は含まれてはいるが、散乱するものがないので青く見えるという点である。
では夕方はなぜ赤い空なのだろう？これは同様にして、太陽光の青い成分が散乱されていくが、昼間と比べ、太陽が傾いているため大気中での光の移動距離が長い。だから、青い光は散乱され尽してしまい、赤い成分しか残らないため空が赤く見える。
END
二回目は素朴な疑問、なんで鉄は触るとひんやりするの？におこたえします。考えてみましょう。鉄と木片を高温槽(ようするに、お風呂）に入れ、十分に時間をおきます。すると、鉄も木片もどちらも高温槽の温度と等しい温度になるはずですね。なんでかって？それは熱力学的に平衡状態に…って、無用に話をややこしくするのはやめましょう。さて、この温度が同じ鉄と木片を触ってみましょう。例えば、温度が１０度であった場合、どちらのほうがより冷たく感じるでしょう鉄ですよね。ではなんで？
そもそも、冷たく感じるというのはどういうことなんでしょう？人間の知覚というものを考えてみましょう。目に見えるというのは、物で光が反射されて、それが目に入ってくるからです。匂いを嗅ぐというのは、人間が匂いとして認識できる物質がある程度の湿り気といっしょに気体として鼻に入るからです。音を聴くというのは、鼓膜で受けた力学的信号を電気的信号に変化して脳で処理する働きです。さて、冷たいとか熱いとか感じるのは？感覚器は皮膚です。触った物質と体の温度差から熱の移動、例えば体温の方が熱いときは体の中の分子のエネルギー、主として運動エネルギーが外の物質の分子へ、又体温のほうが冷たいときはその逆で熱の移動が起こります。この熱の移動が熱い、冷たいと感じる原因です。
いよいよ本題です。なんで鉄と木では冷たさの感じる度合いが違うのか？ここからちょっと難しくなります。量子力学によると、物質の持つエネルギーは飛び飛びの値です。いわゆる量子化されているわけです。そしてその飛び飛びのエネルギー間隔は電子の移動できる距離の二乗に反比例します。つまり、移動できる距離が大きくなればなるほど、エネルギーの間隔は狭くなりエネルギーが連続的に変化できるようにみえてきます。現実的にはその間隔が常温の熱エネルギー（=kT、kはボルツマン定数。Tは常温[K]）よりも小さくなると連続的にみえます。だから高校で習う理科ではエネルギーを連続的にしか取り扱わなかったのは、マクロな視点であることと、比較して常温の熱エネルギーより高いからなんですねぇ。
このことを踏まえると後一息です。鉄のような金属は、その結合が金属結合といって、電子が移動できる範囲は金属内部全体です。これは高校で習う内容ですね。従って電子の移動できる範囲が金属原子にとどまらず、金属全体に広がり、移動可能距離が長くなります。したがってエネルギーが連続的に変化するようにみえます。では木はどうでしょう？木片の主成分は細胞壁のセルロースです。セルロースはグルコース重合体ですが、金属と比べれば電子の移動範囲は狭く（だって分子結合ですからね）、またエネルギーは飛び飛びで温度を上げることのできる電磁波の取りうる波長の範囲は鉄に比べれば狭いです。さてなんでここで電磁波か？高校の物理で習う光電効果とか思い出してくださいね。
要するに、鉄は木と比べて温度変化をできる波長が多い。人間の肌から熱が移動するとき、移動する熱は種々の波長をとります。だから、いろんな波長でもOKな鉄のほうが熱を吸い取りやすいことになり、より冷たく感じるということになりますね。
END
飛行中の飛行機に加わっている力は５つ。水平方向に二つと、鉛直方向に三つ。まず水平方向から考えると、進行方向に加わる力はエンジンからの出力、すなわち推進力。それとは反対方向に加わる力は空気の抵抗力で、速度の二乗と面積の積に比例して大きくなります。従って、この二力のバランスをとれば、前に進みます。
では飛行機が浮く理由を考えましょう。鉛直方向に加わる力は下向きに重力、上向きに揚力と空気の浮力。つまり、揚力と浮力の合力が重力に勝てば、浮きます。さて、まず浮力を考えると、浮力というのは流体中の物体がその体積分の流体と等しい流体の重量を上向きに受ける力のことです。そこで空気の密度を考えると、約1.3×10^(-6)g/cm^3ぐらい（零度一気圧の理想気体）これは金属と比べるとオーダーが10の７乗くらい違うので、飛行機が浮く浮かないの議論の場合ほとんど影響を与えません。よって、以後は揚力と重力の兼ね合いを考えます。
揚力とはベルヌーイの法則から導かれる、流体中で移動する物体が受ける力のことです。ベルヌーイの法則は面倒なので説明しませんが、こう考えるとそのような力が起こるということがわかるだろうとおもいます。翼を横から見ると上に膨らんでいます。ラグビーボールを半分にしたのを想像してください。進行方向からやってくる空気は翼に当たって上と下に分かれます。上に行った空気は下の平らなほうに行った空気と比べ、余計な距離を進まなければならない分、単位時間あたりに翼の上下を通りすぎる空気は上のほうが少なく、下のほうが多くなります。すなわち濃度が下のほうが濃くなります。従って、気圧が下の方が大きくなり、上向きの力が生じます。この揚力は抵抗同様、速さの二乗と面積に比例します。
これらの力の合力で飛行機は浮き、前に進むわけですね。
END
手元に今年度版の野球名鑑があります。突然ですが、選手の身長に注目してみましょう。
やはり、野球選手だけあって、皆さん背が大きいですね。つらつら眺めていくうちにふと気づいたことがあります。
「背がむちゃくちゃ大きい（190cm以上）の選手のほとんどは投手である」
これについて、考察してみましょう
色々考えられますが、第一に思いつくのは
”投手の背が大きいほうが、角度のある球を投げられるから”
たしかに上から投げ下ろされた球をミートするのは難しいですよね。（ドッチボールのジャンプシュートを想像してみるとわかる）
ほかには、
”大きいほうが、ピッチャー返しをとめやすい”
的当てですね。
”位置エネルギーが稼げて、より速い球が投げられる”
これは分かりやすいですよね。ためしに普通の投手の背を180cm、長身選手の背を200cm、二人の腕の長さを60cmとすると、
球速は4.2%アップしました。これは、長身選手の腕をかなり短めに計算しているので、実際はもっとあがると思います。
体格的にも日本人の100mileは無理なのかなぁ...。
さて、じゃあなんで超長身選手は野手にならないのか？野手だとこれらのメリットが活かせない事以外にデメリットがあるのでしょうか？ ここで、”足”に注目してみました。特に足の速さがポイントになります。
投手が足が速い必要はありません。投手の足に必要とされるのは粘りであり、スタミナであるような持久力であり、瞬発力はいりません。 たしかにどの球団にもチームの俊足自慢に名を連ねる投手は必ずいますが、それは投手をするような人はもともと万能選手だからです。
でも、野手はそうじゃありません。打席しかり、捕球しかり。投手とは逆に瞬発力の方が要求されることが多いです。 では、この瞬発力において長身選手は何かデメリットがあるのでしょうか？
そのことを検証するために、外野手を例にとって考えます。いい外野手は足が速い。これは落下地点までに到達する時間が短ければそれだけ敵を刺しやすくなるからです。 この足の速さでさっきと同じように長身選手と普通の選手を比べて見ます。
仮定として 「単位体積あたりの筋肉の力は同じ」（元は同じ人間ですから）を導入します。 すると、足の速さを決定するのはストロークだけになります。さて、このストロークを決定するのは何か？
高校の物理の時間の”振り子の周期”について思い出してください。振り子の周期は
T=2×3.14×{(糸の長さ）/(重力定数）}^(0.5)
で、あらわされます。ここで、糸の長さを足の長さに置き換えると...
T=2×3.14×{(足の長さ）/(重力定数）}^(0.5)
すると足が長ければ長いほど一歩すすむのに時間が余計にかかることになります。
ここで、さっきと同じように計算してみるとだいたい10%くらい差がでます。つまり、背が小さいほうが足が速い。
バスケしかり、野球しかり、背によってポジションが決まる競技はたくさんあるけど、ちゃんと理由があったんですね。
END
エコグラムってごぞんじですか？なんか50くらいの質問に答えて、その結果から回答者の性格なんかを求めるとかいう怪しいものなんですが...、
以下私の結果を載せますね。
貴方が男性の場合なら、かなりバランスの取れた仕事人間のタイプであり、社会的信用やその人物評価も、決して低くは無いでしょう。但し、貴方が女性の場合には、権力志向の強さと共に、物事を決め付けて行く態度が強過ぎ、何でも理屈で割り切って行く傾向が目立つ為に、同性ばかりか異性にまで、一目置かれるような状況が生じ易いでしょう。その場合に、貴方が何か物凄く重い責任を背負った、リーダー的立場なら、まさに打って付けのタイプと云う事になりますが、主婦で有ったり、単なるＯＬで有ったりした場合には、その功罪が半ばする事は、避けられないでしょう。
厳しく異性の品定めをするタイプでしょう。漠然とした選び方をするのでは無く、人間性、学歴、職業、容姿、好みなどに対する動かし難い選定基準が既に存在して居て、その枠に当て填め、篩（ふるい）に掛けて行くと云うような、遣り方をするタイプです。優しさよりも厳しさが、情緒よりも理論が優先して行くタイプですから、それなりのバランスは取れて居るにしても、何処かに隙の無い厳しさや、味気無さが生じて来る事は、否定出来ないでしょう。もし貴方が女性で有った場合には、もう少し柔らかく、ふんわりとした雰囲気を醸（かも）し出すように努力した方が、よりベストでしょう。恋愛や結婚生活の総体的な行動パターンは、やや硬派に属するタイプでしょう。
性格面から見た、職業に対する適応性は、相当に巾が広く、大概の職種なら十分にこなし得るでしょう。但し、宗教家、カウンセラー、ケースワーカーなどの特殊な職業と、これは職業ではありませんが、社会には不可欠のボランティア的社会奉仕家である、民生委員、保護師、刑務所の篤志面接委員などは総合的な性格構成から見て。不適性な面が強いと思われますので、引き受けたりしない方が無難でしょう。
一般的な人付き合いでは、余り理詰めに走ったり、杓子定規（しゃくしじょうぎ）な権利論や義務論を振り回さないように、気をつけた方が良いと思います。自分の物差しで、全ての現象を推し計ろうとしない方が無難です。
どうでした、あたってましたか？
ＥＮＤ
ここで鬼畜度チェックというものをやっていて、私がした結果は以下の通りでした。
あなたは
96.1%
鬼畜でございます(当社比)。
|
ぎりぎり一般人のレベルに残れるかどうかというところです。 しかし一歩間違えば奈落の底へ落ちていくだけです。 というか、落ちていく可柏ｫの方が高いですね。 ここまできたら無駄なあがきをせずに、どっぷり鬼畜化した方が 貴方のために良いかも知れません。 きっと心の奥底ではそれを望んでるハズですよ・・・ いつでもお待ちしていますよ。ニヤリ。 ▼ちょっとあなた、アブナイ思想の持ち主なんじゃないですか？ いくら世の中に不満があっても 武力行使はどうかとおもいますよ 人が死ぬのを見て楽しんだりしそうですね・・・ こわいこわい・・・ |
どうです？あたってますか？
END
しし座流星群の季節です(11/20現在)。今年は昨年と比べ数が少ないみたいですね。話によると1/100とか。流星が発光を始めるのは、大気圏のうちの電離Ｅ層と呼ばれる部分（あとで説明します）です。この部分に流星物質が突入すると、流星物質は温度が上昇し、蒸発して原子まで壊れ、発光します。
このとき、流星の周りの気体が高温のために電離（原子や分子が電子を放出、またはとりいれてイオンになること）するのですが、電離層では空気が希薄なため、一度電離した原子は簡単には再結合せず、電離気体（プラズマといいます）が残ります。
そして、イオンが再結合する過程で出す光が、筋を引いたように見える光、つまり「痕（こん）」になって我々の目に見えるということなのです。
一個ずつ解決していきましょう。
まずなぜ電離するかというと、それは周囲が高温だからです。原子核に引っ張られている電子が離れることができるくらいに。
定性的な不等式を使うと、
｜電子の電気的な位置エネルギー｜≦(外部から熱という形で与えられる運動エネルギー∝T)
(1/4πk)*Ae^2/r^2≦kTです(kはボルツマン定数、Aは原子番号、rは電子と原子核との間の距離、Tは外気の温度)
原子はおそらく水素や酸素だろうから、外気の温度も計算できますが面倒なので割愛。
次になぜ再結合するかというと、それは温度が下がってさっきの不等式を満たせなくなるからです。
自然はより安定な形になろうとしますから、よりエネルギーが安定な形、イオン結合をとります。
最後に再結合するときになぜ発光するか？これが問題。
電離したイオンが再結合するといっても、普通は発光しませんよね？
水に塩を溶かし再結晶させても、電離はしますが、(注.無色透明なので見てもわかりません。せいぜい屈折率の変化くらい)
発光はしません。これは温度が低くて原子が励起してないためです。
この流星の場合、高温のために基底状態から励起状態におかれたために、
降下するうちに冷えて基底状態に戻ります。このときに自分が受け取ったエネルギー分の光(電磁波)を出します。
電磁波の話題がここではよく出てきますが、ではこの蛍光の色はどうか？
写真をみると、赤っぽいですね。でも写真全体が赤っぽいのでおそらく元は白でしょう。
なんで赤いんだろ？写真詳しくないからよくわかりません。
さてではなぜ白か？多分これはさまざまな可視光が混ざり合ったためと思われます。
なにか一色だけだったら物質が特定できるんだけどなぁ。残念、でも計算が面倒か。
END
今日(11/22)はなんの日でしょうか？隣の画像がヒントです。
答え...1963年 アメリカ、ケネディ大統領が遊説先で頭部を狙撃され死亡した日
この事件に関して詳しいのはここです。
さて、JFKの暗殺事件は衛星中継されてしまったことでも名高く、また大統領自身も
インテルサットとよばれる衛星を使った通信に関係が深いです。
そこで今回は衛星に関する数学的な話をします。
通信衛星の第一義的な目的とはなんぞや？それは地上から電磁波という形で送られてきた情報を
指定された地上のポイントに送信することです。
ということは、早い話地球の周りを鏡で覆ってやれば衛星は必要なくなります。
実際にはそういうわけにもいかないので、衛星を一個ずつ打ち上げるのですが、今その最小の個数を考えます。
まず地上が一次元の場合。
このとき、地上は直線になります。ということで、適当な点に衛星をおいてやれば
どこからきた情報でも反射or透過してやることで、任意の場所に送れます。
答え.一個
次に地上が二次元の場合。
このとき、地上は平面になります。ということで、地上とは異なる平面状に一個衛星を置いてやれば
必要十分です。離れれば離れるほど照射角度が厳しくなりますが、今は数学的な話なので気にしません。
答え.一個
さて問題は三次元の場合。
まず地上が球状(真球および楕円球)の場合を考えて見ましょう。
無限遠に衛星を置くことが可能ならば、わずか二個で済みます。理由は下の図参照。
では、無限円に衛星を置くことが許されない現実的な場合を考えます。
極方向に衛星を置かない場合は地上の周囲を衛星が取り囲むような形になります。
このとき、必要な衛星の個数は北半球に三個、南半球に三個で計六個になります。そして当然極に電波は届きません。
この場合の衛星は北緯および南緯四十五度の周りを衛星が取り囲んでいる状態です。
では、極方向に衛星を置く場合を考えて見ましょう。
すると、極に置かれた衛星でカバーできないのは赤道を中心とする帯状の部分です。
ということなので、赤道面上にさっきの要領で三個並べてやればこの帯状の部分もカバーできます。
このとき、必要な個数は五つ。衛星を線分で結んでやれば、合同な三角形を底面に持つ三角錐をひっつけた状態になります。
答え.五個
もし、地上が真球であるならば、衛星をうまく配置してやることで正五面体にすることができます。
このとき、地上はこの立体に内接する球です。
眠くなったので続きはまた今度。次回は私と誕生日が同じケプラーの話題と今回の話の拡張(拡張できたらですが)を予定してます。
END
| 次元 | 衛星の個数 |
|---|---|
| 一次元 | 一個 |
| 二次元 | 三個 |
| 三次元 | 五個 |
さて、これを見ると単純な関係が推測できます。衛星の個数をＳnとするとき、n次元において...
Ｓn=2n-1
という式がなりたちそうです。
これは次のようなイメージをしてやれば考えやすいと思います。
ギターの弦のようなピンと張られた紐を日本考えてください。この紐は一次元の世界を表しています。
これを横から、すなわちこの紐と直交する向きから両方に引っ張ると二次元のスペースができます。
そして引っ張っている指の位置と紐の任意の点に衛星をおけばすべてをカバーすることが出来ます。
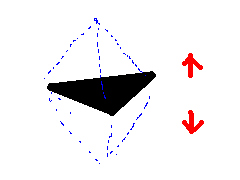次に三角形の形をした二枚のゴム膜を考えてください。この三角形の頂点はピンで固定されています。
このゴム膜を膜と垂直な向きから両方に引っ張ると三次元のスペースができます。
そして引っ張っている指の位置と三角形の頂点に衛星をおけば、すべての空間をカバーできます。
うえのふたつはどちらもこのような表現で言い換えることが出来ます。すなわち、
一つ前の次元の立体を、新たに付け加えられた軸の方向から引っ張れば、その次元における衛星の状態が決まる。
次元の話はこのくらいにして、次回はケプラーと正多面体の関係について述べたいと思います。
END